In this series of articles, we will introduce the Heston model: a well-known stochastic volatility model that removes the constant volatility assumption encountered in the Black-Scholes model. In the first part, we will start by introducing the Black-Scholes model and illustrate why the constant volatility assumption is generally not observed on option markets. Then, in the second part we will state the Heston model before moving to pratical considerations with model calibration in the third and last part of this series.
Part I: The Black-Scholes model and the constant volatility assumption
Black Scholes model:
On options markets, the Black-Scholes (1973) model constitutes the bedrock of option pricing theory. In this model, the dynamic of the underlying asset under the risk-neutral measure is described with the following stochastic differential equation:
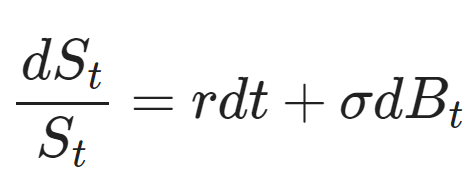
with S the value of the underlying asset, r the risk-free rate, σ the volatility and B a Brownian motion. Additional assumptions are made: existence of a risk-free rate, no dividends, no arbitrage opportunity, ability to borrow and lend cash at the risk-free rate, ability to buy and sell any amount of the underlying asset, and finally a frictionless market.
The solution at t for a call option with strike price K and maturity T is given by the Black-Scholes formula:
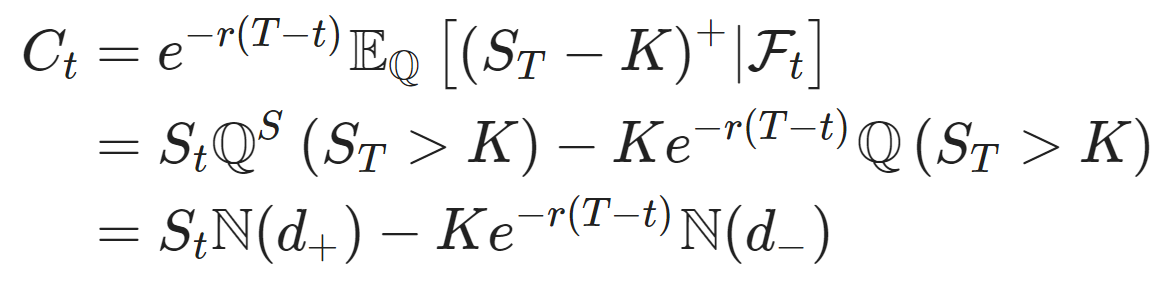
with 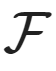 the natural filtration,
the natural filtration,  the risk-neutral measure and
the risk-neutral measure and 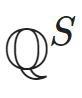 the stock measure. We also have :
the stock measure. We also have :
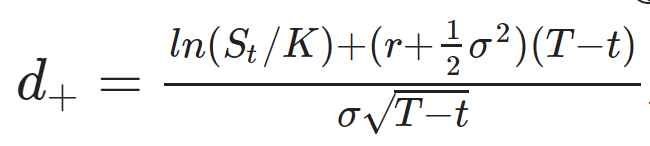
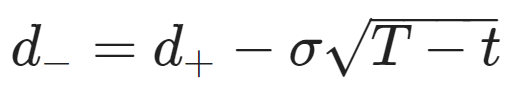
and N is the cumulative distribution function of the standard Normal distribution. Please refer to classical textbooks for a complete derivation (for example Shreve (2004)).
Is volatility constant ?
In the Black-Scholes model, the volatility is assumed constant, which is a simplifying assumption. Indeed, several stylized facts describe a proper dynamic to the volatility. For instance, in Cont (2001), it is shown that volatility exhibits clustering properties with periods of high volatility and periods of low volatility; volatility is also observed as negatively correlated with asset returns (so-called leverage effect).
Figure 1: SPX daily log-returns and associated realized volatility (estimated on a rolling 30 days window)
Another way to visualize the limitations of the Black-Scholes model is to compute the implied volatility, that is, the volatility to input in the Black-Scholes model to produce the quoted price for a given expiration date and a strike price. By computing the implied volatility for each expiration dates and all strike prices, we obtain an implied volatility surface. In the Black-Scholes framework, one would expect a constant volatility across strike prices for a given expiration date, however, this behavior is typically not observed.
Figure 2: SPX implied volatility surface
In the heat map above, the Y-axis is the time to expiry and the X-axis is the moneyness, while the implied volatilities can be read from the colored scale. We can see the implied volatility for out of the money (OTM) options is greater than the implied volatility for at the money (ATM) options; deep in the money (ITM) options also exhibit moderately higher volatilities. This phenomenon is what is frequently referred as volatility smile/smirk. Moreover, as we progress on longer maturities, the implied volatility smiles become less and less marked.
In both cases, the Black-Scholes model lacks additional degrees of freedom to produce such behaviors. Many extensions have been built upon the Black-Scholes model in order to get more precise models by adding jumps, local volatility, stochastic volatility or even combinations of them. Each one of these types of models have their own benefits and drawbacks and in the next article, we will review the Heston model, a stochastic volatility model.
References:
- F. Black, M. Scholes (1973). "The Pricing of Options and Corporate Liabilities". Journal of Political Economy. 81 (3):637–654.
- R. Cont (2001). "Empirical properties of asset returns: Stylized facts and statistical issues". Quantitative Finance. 1 (2):223–236.
- S. Shreve (2004). "Stochastic calculus for finance II: Continuous-time models". Springer.
 BLOGGING
BLOGGING

